공부자료) 기어의 치형
- 탑맨
- 1816
- 0
첨부 3
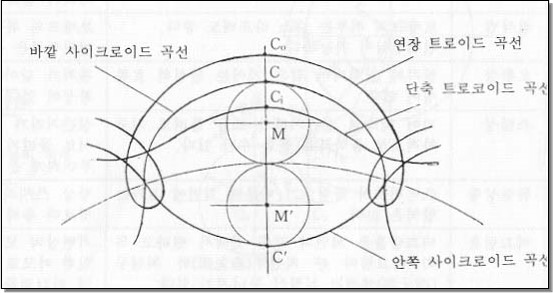
사이크로이드 곡선은 큰 원 주위를 작은 원이 굴러갈 때 작은 원 상의 한 점 C가 그리는 궤적이다. 특히 원주를 벗어난 점이 그리는 궤적을 트로코이드(Trocoid) 곡선이라 부른다.
그림에서 보듯이 원 M이 원 O의 바깥측을 굴러갈 때 그리는 곡선을 외사이크로이드(Epi-Cycloid)라 부르고, 원 O의 안쪽을 따라 굴러갈 때 그리는 사이크로이드를 내사이크로이드(Hypo-Cycloid)라 부른다
2. 인볼루트(Involute) 곡선
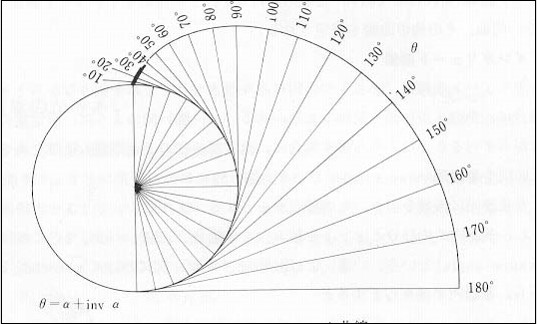
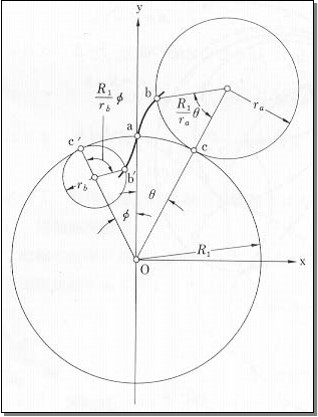
인볼루트 치형은 외사이크로이드 곡선에서 큰 원 주위를 구르는 작은 원의 반경이 무한대로 되면서 굴러가는 경우, 작은 원 상의 한 점이 그리는 궤적이다.
다시 말하면 직선이 원O 위를 구를 때 직선의 끝점이 그리는 궤적을 인볼루트 곡선이라 부른다. 이것은 마치 원통에 실을 감아서 실을 팽팽하게 잡아 당기면서 풀어나갈 대 실의 끝이 그리는 궤적과 같다.
인볼루트 곡선은 원 O의 바깥 쪽을 직선이 구를 때 그리는 궤적이므로 원 O의 안쪽에는 존재하지 않는다. 이 원을 인볼루트의 기초원(Base circle)이라 부른다.
공유
